–†–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ–Β–Ϋ–Η–Β ―¹–≤–Β―²–Α –Ω–Ψ –≤–Ψ–Μ–Ψ–Κ–Ϋ―É
–û―¹–Ϋ–Ψ–≤–Ϋ―΄–Φ–Η ―³–Α–Κ―²–Ψ―Ä–Α–Φ–Η, –≤–Μ–Η―è―é―â–Η–Φ–Η –Ϋ–Α ―Ö–Α―Ä–Α–Κ―²–Β―Ä ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ–Β–Ϋ–Η―è ―¹–≤–Β―²–Α –≤ –≤–Ψ–Μ–Ψ–Κ–Ϋ–Β, –Ϋ–Α―Ä―è–¥―É ―¹ –¥–Μ–Η–Ϋ–Ψ–Ι –≤–Ψ–Μ–Ϋ―΄ –Η–Ζ–Μ―É―΅–Β–Ϋ–Η―è, ―è–≤–Μ―è―é―²―¹―è: –≥–Β–Ψ–Φ–Β―²―Ä–Η―΅–Β―¹–Κ–Η–Β –Ω–Α―Ä–Α–Φ–Β―²―Ä―΄ –≤–Ψ–Μ–Ψ–Κ–Ϋ–Α; –Ζ–Α―²―É―Ö–Α–Ϋ–Η–Β; –¥–Η―¹–Ω–Β―Ä―¹–Η―è.
–™–Β–Ψ–Φ–Β―²―Ä–Η―΅–Β―¹–Κ–Η–Β –Ω–Α―Ä–Α–Φ–Β―²―Ä―΄ –≤–Ψ–Μ–Ψ–Κ–Ϋ–Α
–û―²–Ϋ–Ψ―¹–Η―²–Β–Μ―¨–Ϋ–Α―è ―Ä–Α–Ζ–Ϋ–Ψ―¹―²―¨ –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ–Β–Ι –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è. –£–Ψ–Μ–Ψ–Κ–Ϋ–Ψ ―¹–Ψ―¹―²–Ψ–Η―² –Η–Ζ ―¹–Β―Ä–¥―Ü–Β–≤–Η–Ϋ―΄ –Η –Ψ–±–Ψ–Μ–Ψ―΅–Κ–Η. –û–±–Ψ–Μ–Ψ―΅–Κ–Α –Ψ–Κ―Ä―É–Ε–Α–Β―² –Ψ–Ω―²–Η―΅–Β―¹–Κ–Η –±–Ψ–Μ–Β–Β –Ω–Μ–Ψ―²–Ϋ―É―é ―¹–Β―Ä–¥―Ü–Β–≤–Η–Ϋ―É, ―è–≤–Μ―è―é―â―É―é―¹―è ―¹–≤–Β―²–Ψ–Ϋ–Β―¹―É―â–Β–Ι ―΅–Α―¹―²―¨―é –≤–Ψ–Μ–Ψ–Κ–Ϋ–Α. –ë―É–¥–Β–Φ –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Α―²―¨ ―΅–Β―Ä–Β–Ζ n1 –Η n2 –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ–Η –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è ―¹–Β―Ä–¥―Ü–Β–≤–Η–Ϋ―΄ –Η –Ψ–±–Ψ–Μ–Ψ―΅–Κ–Η, ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –û–¥–Η–Ϋ –Η–Ζ –≤–Α–Ε–Ϋ―΄―Ö –Ω–Α―Ä–Α–Φ–Β―²―Ä–Ψ–≤, –Κ–Ψ―²–Ψ―Ä―΄–Ι ―Ö–Α―Ä–Α–Κ―²–Β―Ä–Η–Ζ―É–Β―² –≤–Ψ–Μ–Ψ–Κ–Ϋ–Ψ, ―ç―²–Ψ — –Ψ―²–Ϋ–Ψ―¹–Η―²–Β–Μ―¨–Ϋ–Α―è ―Ä–Α–Ζ–Ϋ–Ψ―¹―²―¨ –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ–Β–Ι –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è Έî: Έî=(n21-n22)/2n21
–ï―¹–Μ–Η –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¨ –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è –Ψ–±–Ψ–Μ–Ψ―΅–Κ–Η –≤―΄–±–Η―Ä–Α–Β―²―¹―è –≤―¹–Β–≥–¥–Α –Ω–Ψ―¹―²–Ψ―è–Ϋ–Ϋ–Ψ–Ι –≤–Β–Μ–Η―΅–Η–Ϋ–Ψ–Ι, ―²–Ψ –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¨ –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è ―¹–Β―Ä–¥―Ü–Β–≤–Η–Ϋ―΄ –≤ –Ψ–±―â–Β–Φ ―¹–Μ―É―΅–Α–Β –Φ–Ψ–Ε–Β―² –Ζ–Α–≤–Η―¹–Β―²―¨ –Ψ―² ―Ä–Α–¥–Η―É―¹–Α. –£ ―ç―²–Ψ–Φ ―¹–Μ―É―΅–Α–Β –¥–Μ―è –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ–Η―è ―Ä–Α–Ζ–Μ–Η―΅–Ϋ―΄―Ö –Ψ―Ü–Β–Ϋ–Ψ–Κ –Ω–Α―Ä–Α–Φ–Β―²―Ä–Ψ–≤ –≤–Ψ–Μ–Ψ–Κ–Ϋ–Α –≤ –Φ–Β―¹―²–Ψ n1 –Η―¹–Ω–Ψ–Μ―¨–Ζ―É―é―² n1eff.
–†–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ–Β–Ϋ–Η–Β ―¹–≤–Β―²–Α –Ω–Ψ –≤–Ψ–Μ–Ψ–Κ–Ϋ―É –Φ–Ψ–Ε–Ϋ–Ψ –Ψ–±―ä―è―¹–Ϋ–Η―²―¨ –Ϋ–Α –Ψ―¹–Ϋ–Ψ–≤–Β –Ω―Ä–Η–Ϋ―Ü–Η–Ω–Α –Ω–Ψ–Μ–Ϋ–Ψ–≥–Ψ –≤–Ϋ―É―²―Ä–Β–Ϋ–Ϋ–Β–≥–Ψ –Ψ―²―Ä–Α–Ε–Β–Ϋ–Η―è, –≤―΄―²–Β–Κ–Α―é―â–Β–≥–Ψ –Η–Ζ –Ζ–Α–Κ–Ψ–Ϋ–Α –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è ―¹–≤–Β―²–Α –Γ–Ϋ–Β–Μ–Μ–Η―É―¹–Α: n1sinΈ‰1 = n2sinΈ‰2
–≥–¥–Β n1 — –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¨ –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è ―¹―Ä–Β–¥―΄ 1, Έ‰1— ―É–≥–Ψ–Μ –Ω–Α–¥–Β–Ϋ–Η―è, n2 — –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¨ –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è ―¹―Ä–Β–¥―΄ 2, Έ‰2 — ―É–≥–Ψ–Μ –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è.
–Λ–Ψ―Ä–Φ–Α–Μ―¨–Ϋ―΄–Β –≤―΄–Κ–Μ–Α–¥–Κ–Η ―É–¥–Ψ–±–Ϋ–Β–Β –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–¥–Η―²―¨ –¥–Μ―è ―¹―²―É–Ω–Β–Ϋ―΅–Α―²–Ψ–≥–Ψ –≤–Ψ–Μ–Ψ–Κ–Ϋ–Α (–≤–Ψ–Μ–Ψ–Κ–Ϋ–Α ―¹–Ψ ―¹―²―É–Ω–Β–Ϋ―΅–Α―²―΄–Φ –Ω―Ä–Ψ―³–Η–Μ–Β–Φ –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―è –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è), –≤ –Κ–Ψ―²–Ψ―Ä–Ψ–Φ –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¨ –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è ―¹–Β―Ä–¥―Ü–Β–≤–Η–Ϋ―΄ ―è–≤–Μ―è–Β―²―¹―è –Ω–Ψ―¹―²–Ψ―è–Ϋ–Ϋ–Ψ–Ι –≤–Β–Μ–Η―΅–Η–Ϋ–Ψ–Ι (n2 =const). –ù–Α ―Ä–Η―¹. 2.2 –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ ―Ö–Ψ–¥ –Μ―É―΅–Β–Ι –≤ ―²–Α–Κ–Ψ–Φ –≤–Ψ–Μ–Ψ–Κ–Ϋ–Β. –Δ–Α–Κ –Κ–Α–Κ ―¹–Β―Ä–¥―Ü–Β–≤–Η–Ϋ–Α ―è–≤–Μ―è–Β―²―¹―è –Ψ–Ω―²–Η―΅–Β―¹–Κ–Η –±–Ψ–Μ–Β–Β –Ω–Μ–Ψ―²–Ϋ–Ψ–Ι ―¹―Ä–Β–¥–Ψ–Ι –Ω–Ψ –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η―é –Κ –Ψ–±–Ψ–Μ–Ψ―΅–Κ–Β (n1 > n2), ―²–Ψ ―¹―É―â–Β―¹―²–≤―É–Β―² –Κ―Ä–Η―²–Η―΅–Β―¹–Κ–Η–Ι ―É–≥–Ψ–Μ –Ω–Α–¥–Β–Ϋ–Η―è Έ‰C — –≤–Ϋ―É―²―Ä–Β–Ϋ–Ϋ–Η–Ι ―É–≥–Ψ–Μ –Ω–Α–¥–Β–Ϋ–Η―è –Ϋ–Α –≥―Ä–Α–Ϋ–Η―Ü―É, –Ω―Ä–Η –Κ–Ψ―²–Ψ―Ä–Ψ–Φ –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Ϋ―΄–Ι –Μ―É―΅ –Η–¥–Β―² –≤–¥–Ψ–Μ―¨ –≥―Ä–Α–Ϋ–Η―Ü―΄ ―¹―Ä–Β–¥ (Έ‰2 = 90¬Α). –‰–Ζ –Ζ–Α–Κ–Ψ–Ϋ–Α –Γ–Ϋ–Β–Μ–Μ–Η―É―¹–Α –Μ–Β–≥–Κ–Ψ –Ϋ–Α–Ι―²–Η ―ç―²–Ψ―² –Κ―Ä–Η―²–Η―΅–Β―¹–Κ–Η–Ι ―É–≥–Ψ–Μ –Ω–Α–¥–Β–Ϋ–Η―è: Έ‰c =arcsin(n2/n1).
–ï―¹–Μ–Η ―É–≥–Ψ–Μ –Ω–Α–¥–Β–Ϋ–Η―è –Ϋ–Α –≥―Ä–Α–Ϋ–Η―Ü―É ―Ä–Α–Ζ–¥–Β–Μ–Α –Φ–Β–Ϋ―¨―à–Β –Κ―Ä–Η―²–Η―΅–Β―¹–Κ–Ψ–≥–Ψ ―É–≥–Μ–Α –Ω–Α–¥–Β–Ϋ–Η―è (–Μ―É―΅ 2), ―²–Ψ –Ω―Ä–Η –Κ–Α–Ε–¥–Ψ–Φ –≤–Ϋ―É―²―Ä–Β–Ϋ–Ϋ–Β–Φ –Ψ―²―Ä–Α–Ε–Β–Ϋ–Η–Η ―΅–Α―¹―²―¨ ―ç–Ϋ–Β―Ä–≥–Η–Η ―Ä–Α―¹―¹–Β–Η–≤–Α–Β―²―¹―è –Ϋ–Α―Ä―É–Ε―É –≤ –≤–Η–¥–Β –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Ϋ–Ψ–≥–Ψ –Μ―É―΅–Α, ―΅―²–Ψ –Ω―Ä–Η–≤–Ψ–¥–Η―² –≤ –Κ–Ψ–Ϋ–Β―΅–Ϋ–Ψ–Φ –Η―²–Ψ–≥–Β –Κ –Ζ–Α―²―É―Ö–Α–Ϋ–Η―é ―¹–≤–Β―²–Α. –ï―¹–Μ–Η –Ε–Β ―É–≥–Ψ–Μ –Ω–Α–¥–Β–Ϋ–Η―è –±–Ψ–Μ―¨―à–Β –Κ―Ä–Η―²–Η―΅–Β―¹–Κ–Ψ–≥–Ψ ―É–≥–Μ–Α (–Μ―É―΅ 1), ―²–Ψ –Ω―Ä–Η –Κ–Α–Ε–¥–Ψ–Φ –Ψ―²―Ä–Α–Ε–Β–Ϋ–Η–Η –Ψ―² –≥―Ä–Α–Ϋ–Η―Ü―΄ –≤―¹―è ―ç–Ϋ–Β―Ä–≥–Η―è –≤–Ψ–Ζ–≤―Ä–Α―â–Α–Β―²―¹―è –Ψ–±―Ä–Α―²–Ϋ–Ψ –≤ ―¹–Β―Ä–¥―Ü–Β–≤–Η–Ϋ―É –±–Μ–Α–≥–Ψ–¥–Α―Ä―è –Ω–Ψ–Μ–Ϋ–Ψ–Φ―É –≤–Ϋ―É―²―Ä–Β–Ϋ–Ϋ–Β–Φ―É –Ψ―²―Ä–Α–Ε–Β–Ϋ–Η―é.
–¦―É―΅–Η, ―²―Ä–Α–Β–Κ―²–Ψ―Ä–Η–Η –Κ–Ψ―²–Ψ―Ä―΄―Ö –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Μ–Β–Ε–Α―² –≤ –Ψ–Ω―²–Η―΅–Β―¹–Κ–Η –±–Ψ–Μ–Β–Β –Ω–Μ–Ψ―²–Ϋ–Ψ–Ι ―¹―Ä–Β–¥–Β, –Ϋ–Α–Ζ―΄–≤–Α―é―²―¹―è –Ϋ–Α–Ω―Ä–Α–≤–Μ―è–Β–Φ―΄–Φ–Η. –ü–Ψ―¹–Κ–Ψ–Μ―¨–Κ―É ―ç–Ϋ–Β―Ä–≥–Η―è –≤ –Ϋ–Α–Ω―Ä–Α–≤–Μ―è–Β–Φ―΄―Ö –Μ―É―΅–Α―Ö –Ϋ–Β ―Ä–Α―¹―¹–Β–Η–≤–Α–Β―²―¹―è –Ϋ–Α―Ä―É–Ε―É, ―²–Α–Κ–Η–Β –Μ―É―΅–Η –Φ–Ψ–≥―É―² ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―è―²―¨―¹―è –Ϋ–Α –±–Ψ–Μ―¨―à–Η–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η―è.

–†–Η―¹ 2.2 — –Ξ–Ψ–¥ –Μ―É―΅–Β–Ι –≤ –Φ–Ϋ–Ψ–≥–Ψ–Φ–Ψ–¥–Ψ–≤–Ψ–Ι –Ψ–Ω―²–Η―΅–Β―¹–Κ–Ψ–Φ –≤–Ψ–Μ–Ψ–Κ–Ϋ–Β ―¹–Ψ ―¹―²―É–Ω–Β–Ϋ―΅–Α―²–Ψ–Φ –Ω―Ä–Ψ―³–Η–Μ–Β–Φ
–ß–Η―¹–Μ–Ψ–≤–Α―è –Α–Ω–Β―Ä―²―É―Ä–Α. –£–Α–Ε–Ϋ―΄–Φ –Ω–Α―Ä–Α–Φ–Β―²―Ä–Ψ–Φ, ―Ö–Α―Ä–Α–Κ―²–Β―Ä–Η–Ζ―É―é―â–Η–Φ –≤–Ψ–Μ–Ψ–Κ–Ϋ–Ψ,
―è–≤–Μ―è–Β―²―¹―è ―΅–Η―¹–Μ–Ψ–≤–Α―è –Α–Ω–Β―Ä―²―É―Ä–Α NA. –û–Ϋ–Α ―¹–≤―è–Ζ–Α–Ϋ–Α ―¹ –Φ–Α–Κ―¹–Η–Φ–Α–Μ―¨–Ϋ―΄–Φ ―É–≥–Μ–Ψ–Φ Έ‰A –≤–≤–Ψ–¥–Η–Φ–Ψ–≥–Ψ–≤ –≤–Ψ–Μ–Ψ–Κ–Ϋ–Ψ –Η–Ζ–Μ―É―΅–Β–Ϋ–Η―è –Η–Ζ ―¹–≤–Ψ–±–Ψ–¥–Ϋ–Ψ–≥–Ψ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Α, –Ω―Ä–Η –Κ–Ψ―²–Ψ―Ä–Ψ–Φ ―¹–≤–Β―² –Η―¹–Ω―΄―²―΄–≤–Α–Β―² –Ω–Ψ–Μ–Ϋ–Ψ–Β –≤–Ϋ―É―²―Ä–Β–Ϋ–Ϋ–Β–Β –Ψ―²―Ä–Α–Ε–Β–Ϋ–Η–Β –Η ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―è–Β―²―¹―è –Ω–Ψ –≤–Ψ–Μ–Ψ–Κ–Ϋ―É, ―³–Ψ―Ä–Φ―É–Μ–Ψ–Ι: NA = sin ΈΗA
–Λ–Η―Ä–Φ―΄-–Η–Ζ–≥–Ψ―²–Ψ–≤–Η―²–Β–Μ–Η –≤–Ψ–Μ–Ψ–Κ–Ϋ–Α ―ç–Κ―¹–Ω–Β―Ä–Η–Φ–Β–Ϋ―²–Α–Μ―¨–Ϋ–Ψ –Η–Ζ–Φ–Β―Ä―è―é―² ―É–≥–Ψ–Μ 9–¥ –Η ―É–Κ–Α–Ζ―΄–≤–Α―é―² ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤―É―é―â–Β–Β –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β ―΅–Η―¹–Μ–Ψ–≤–Ψ–Ι –Α–Ω–Β―Ä―²―É―Ä―΄ –¥–Μ―è –Κ–Α–Ε–¥–Ψ–≥–Ψ –Ω–Ψ―¹―²–Α–≤–Μ―è–Β–Φ–Ψ–≥–Ψ ―²–Η–Ω–Α –≤–Ψ–Μ–Ψ–Κ–Ϋ–Α.
–ù–Ψ―Ä–Φ–Η―Ä–Ψ–≤–Α–Ϋ–Ϋ–Α―è ―΅–Α―¹―²–Ψ―²–Α. –î―Ä―É–≥–Η–Φ –≤–Α–Ε–Ϋ―΄–Φ –Ω–Α―Ä–Α–Φ–Β―²―Ä–Ψ–Φ, ―Ö–Α―Ä–Α–Κ―²–Β―Ä–Η–Ζ―É―é―â–Η–Φ –≤–Ψ–Μ–Ψ–Κ–Ϋ–Ψ –Η ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―è―é―â–Η–Ι―¹―è –Ω–Ψ –Ϋ–Β–Φ―É ―¹–≤–Β―², ―è–≤–Μ―è–Β―²―¹―è –Ϋ–Ψ―Ä–Φ–Η―Ä–Ψ–≤–Α–Ϋ–Ϋ–Α―è ―΅–Α―¹―²–Ψ―²–Α V, –Κ–Ψ―²–Ψ―Ä–Α―è –Ψ–Ω―Ä–Β–¥–Β–Μ―è–Β―²―¹―è –Κ–Α–Κ V=œÄβ΄Ödβ΄ÖNA/ΈΜ
–ù–Ψ–Φ–Β–Ϋ–Κ–Μ–Α―²―É―Ä–Α –Φ–Ψ–¥. –ü―Ä–Η –±–Ψ–Μ–Β–Β ―¹―²―Ä–Ψ–≥–Ψ–Φ ―Ä–Α―¹―¹–Φ–Ψ―²―Ä–Β–Ϋ–Η–Η –Ω―Ä–Ψ―Ü–Β―¹―¹–Α ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ–Β–Ϋ–Η―è ―¹–≤–Β―²–Α –Ω–Ψ –≤–Ψ–Μ–Ψ–Κ–Ϋ―É ―¹–Μ–Β–¥―É–Β―² ―Ä–Β―à–Α―²―¨ –≤–Ψ–Μ–Ϋ–Ψ–≤―΄–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è –€–Α–Κ―¹–≤–Β–Μ–Μ–Α. –‰–Φ–Β–Ϋ–Ϋ–Ψ –≤ ―ç―²–Ψ–Ι ―²―Ä–Α–Κ―²–Ψ–≤–Κ–Β –Μ―É―΅–Η –Α―¹―¹–Ψ―Ü–Η–Η―Ä―É―é―²―¹―è ―¹ –≤–Ψ–Μ–Ϋ–Α–Φ–Η, –Ω―Ä–Η―΅–Β–Φ ―Ä–Α–Ζ–Μ–Η―΅–Ϋ―΄–Β ―²–Η–Ω―΄ –≤–Ψ–Μ–Ϋ — ―Ä–Β―à–Β–Ϋ–Η―è ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι — –Ϋ–Α–Ζ―΄–≤–Α―é―²―¹―è –Φ–Ψ–¥–Α–Φ–Η.
–ü–Ψ –≤–Ψ–Μ–Ψ–Κ–Ϋ―É –Φ–Ψ–≥―É―² ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―è―²―¨―¹―è –Κ–Α–Κ ―²–Ψ–Μ―¨–Κ–Ψ –Ψ–¥–Ϋ–Α –Φ–Ψ–¥–Α — –Ψ–¥–Ϋ–Ψ–Φ–Ψ–¥–Ψ–≤―΄–Ι ―Ä–Β–Ε–Η–Φ, ―²–Α–Κ –Η –Φ–Ϋ–Ψ–≥–Ψ –Φ–Ψ–¥ — –Φ–Ϋ–Ψ–≥–Ψ–Φ–Ψ–¥–Ψ–≤―΄–Ι ―Ä–Β–Ε–Η–Φ. –€–Ϋ–Ψ–≥–Ψ–Φ–Ψ–¥–Ψ–≤―΄–Ι –Η–Μ–Η –Ψ–¥–Ϋ–Ψ–Φ–Ψ–¥–Ψ–≤―΄–Ι ―Ö–Α―Ä–Α–Κ―²–Β―Ä –Η–¥―É―â–Β–≥–Ψ –Ω–Ψ –≤–Ψ–Μ–Ψ–Κ–Ϋ―É ―¹–≤–Β―²–Α –Κ–Ψ―Ä–Β–Ϋ–Ϋ―΄–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ –≤–Μ–Η―è–Β―² –Ϋ–Α –¥–Η―¹–Ω–Β―Ä―¹–Η―é, –Α ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, –Η –Ϋ–Α –Ω―Ä–Ψ–Ω―É―¹–Κ–Ϋ―É―é ―¹–Ω–Ψ―¹–Ψ–±–Ϋ–Ψ―¹―²―¨ –≤–Ψ–Μ–Ψ–Κ–Ϋ–Α. –û―²–Φ–Β―²–Η–Φ, ―΅―²–Ψ –Ϋ–Ψ―Ä–Φ–Η―Ä–Ψ–≤–Α–Ϋ–Ϋ–Α―è ―΅–Α―¹―²–Ψ―²–Α ―è–≤–Ϋ–Ψ –Ζ–Α–≤–Η―¹–Η―² –Ψ―² –¥–Μ–Η–Ϋ―΄ –≤–Ψ–Μ–Ϋ―΄ ―¹–≤–Β―²–Α.
–ù–Α ―Ä–Η―¹. 2.3 –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Α –Ψ–±―â–Α―è –Κ–Α―Ä―²–Η–Ϋ–Α ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ–Β–Ϋ–Η―è ―¹–≤–Β―²–Α –Ω–Ψ ―Ä–Α–Ζ–Ϋ―΄–Φ ―²–Η–Ω–Α–Φ
―¹–≤–Β―²–Ψ–≤–Ψ–¥–Ψ–≤: –Φ–Ϋ–Ψ–≥–Ψ–Φ–Ψ–¥–Ψ–≤–Ψ–Φ―É ―¹―²―É–Ω–Β–Ϋ―΅–Α―²–Ψ–Φ―É, –Φ–Ϋ–Ψ–≥–Ψ–Φ–Ψ–¥–Ψ–≤–Ψ–Φ―É –≥―Ä–Α–¥–Η–Β–Ϋ―²–Ϋ–Ψ–Φ―É, –Η
–Ψ–¥–Ϋ–Ψ–Φ–Ψ–¥–Ψ–≤–Ψ–Φ―É ―¹―²―É–Ω–Β–Ϋ―΅–Α―²–Ψ–Φ―É –≤–Ψ–Μ–Ψ–Κ–Ϋ―É.
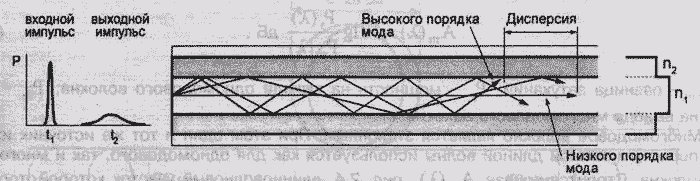
–†–Η―¹ 2.3 — –†–Α―¹–Ω―Ä–Α―¹―²―Ä–Β–Ϋ–Β–Ϋ–Η–Β ―¹–≤–Β―²–Α –Ω–Ψ –Φ–Ϋ–Ψ–≥–Ψ–Φ–Ψ–¥–Ψ–≤–Ψ–Φ―É ―¹―²―É–Ω–Β–Ϋ―΅–Α―²–Ψ–Φ―É –≤–Ψ–Μ–Ψ–Κ–Ϋ―É.
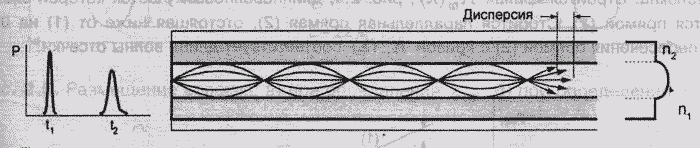
–†–Η―¹ 2.4 — –†–Α―¹–Ω―Ä–Α―¹―²―Ä–Β–Ϋ–Β–Ϋ–Η–Β ―¹–≤–Β―²–Α –Ω–Ψ –Φ–Ϋ–Ψ–≥–Ψ–Φ–Ψ–¥–Ψ–≤–Ψ–Φ―É –≥―Ä–Α–¥–Η–Β–Ϋ―²–Ϋ–Ψ–Φ―É –≤–Ψ–Μ–Ψ–Κ–Ϋ―É

–†–Η―¹ 2.5 — –†–Α―¹–Ω―Ä–Α―¹―²―Ä–Β–Ϋ–Β–Ϋ–Η–Β ―¹–≤–Β―²–Α –Ω–Ψ –Ψ–¥–Ϋ–Ψ–Φ–Ψ–¥–Ψ–≤–Ψ–Φ―É ―¹―²―É–Ω–Β–Ϋ―΅–Α―²–Ψ–Φ―É –≤–Ψ–Μ–Ψ–Κ–Ϋ―É